




Clear[getAuthorsForPaper];
stringCleanupRules = {"ü" -> "u", "Henry Tye" -> "Tye, Henry"};
getAuthorsForPaper[recid_] :=
Module[ {header =
"http://inspirehep.net/search?ln=en&ln=en&p=refersto%3Arecid%3A" <>
ToString[recid] <>
"&of=xe&action_search=Search&sf=&so=d&rm=&rg=250", firstBatch,
cnt = 0, numRecs, data, allAuthors, countAuthors, t},
t = AbsoluteTiming[
data = {Import[header <> "&sc=0", "XML"]};][[1]];
numRecs =
StringSplit[data[[1, 1, -1, -1]], " "][[-1]] // ToExpression;
StylePrint[
"Looks like " <> ToString[numRecs] <> " cites. You've got a " <>
ToString[Round[(numRecs - 250)*t/250/6]/10.] <>
" minute wait to finish downloading."];
While[numRecs > (cnt += 250),
data = Append[data,
Import[header <> "&jrec=" <> ToString[cnt + 1], "XML"]];];
allAuthors = (StringSplit[#,
","][[1]] & /@ (Reap[# /.
XMLElement["author", a___] :>
Sow[StringReplace[#, stringCleanupRules] & /@ {a}]] //
Last // Flatten)) & /@ data // Flatten;
countAuthors = (allAuthors // Tally);
Map[Style[#[[1]], {FontSize ->
14 + #[[2]] - Mean[countAuthors[[All, 2]]],
ColorData["CMYKColors"][#[[2]]/Max[countAuthors[[All, 2]]]],
Bold}] &, countAuthors // Sort]
]
compare with Gist include and default rendering:
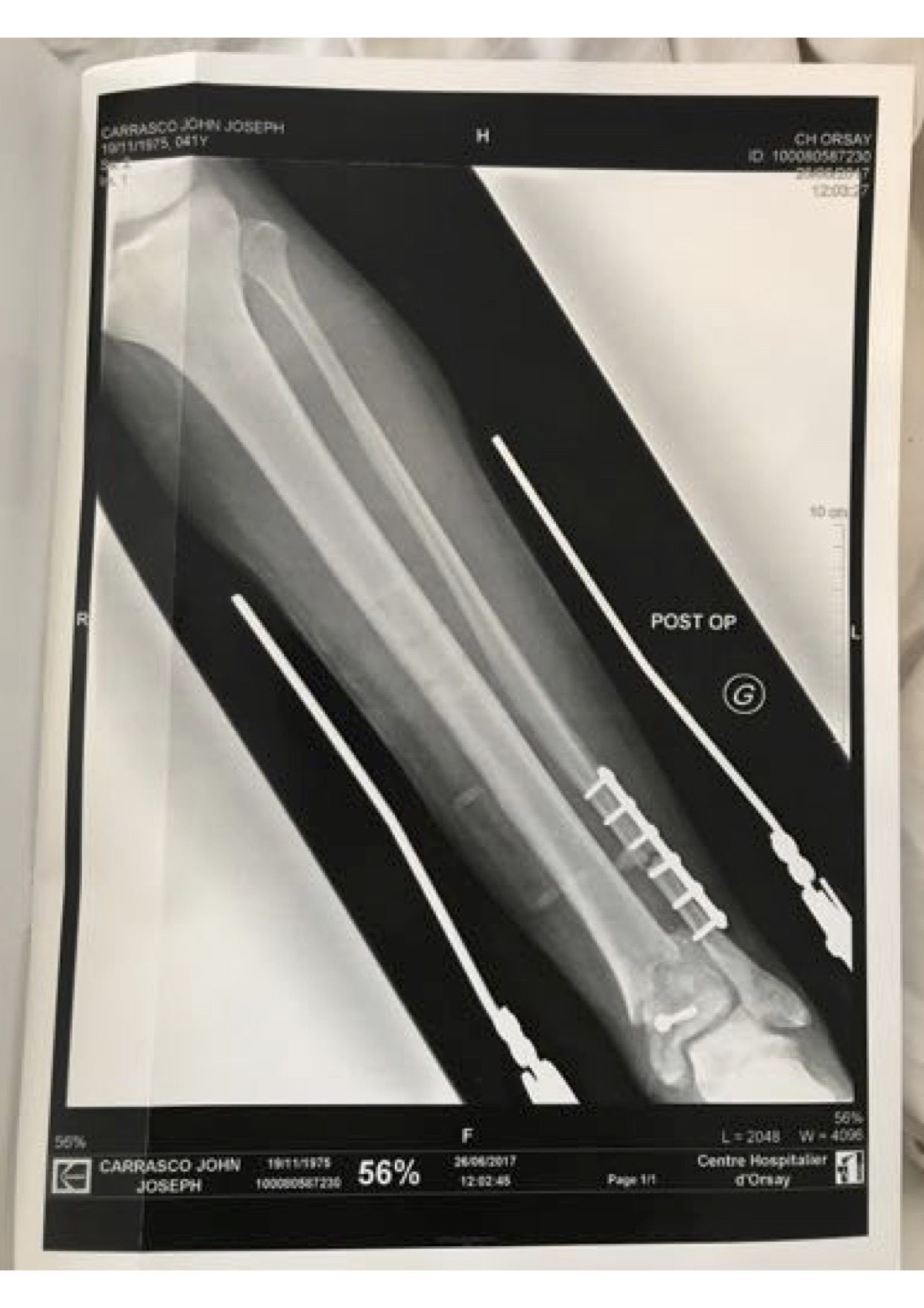
]]>External hardware removed a few weeks ago (day before leaving to Israel for Strings 2017).
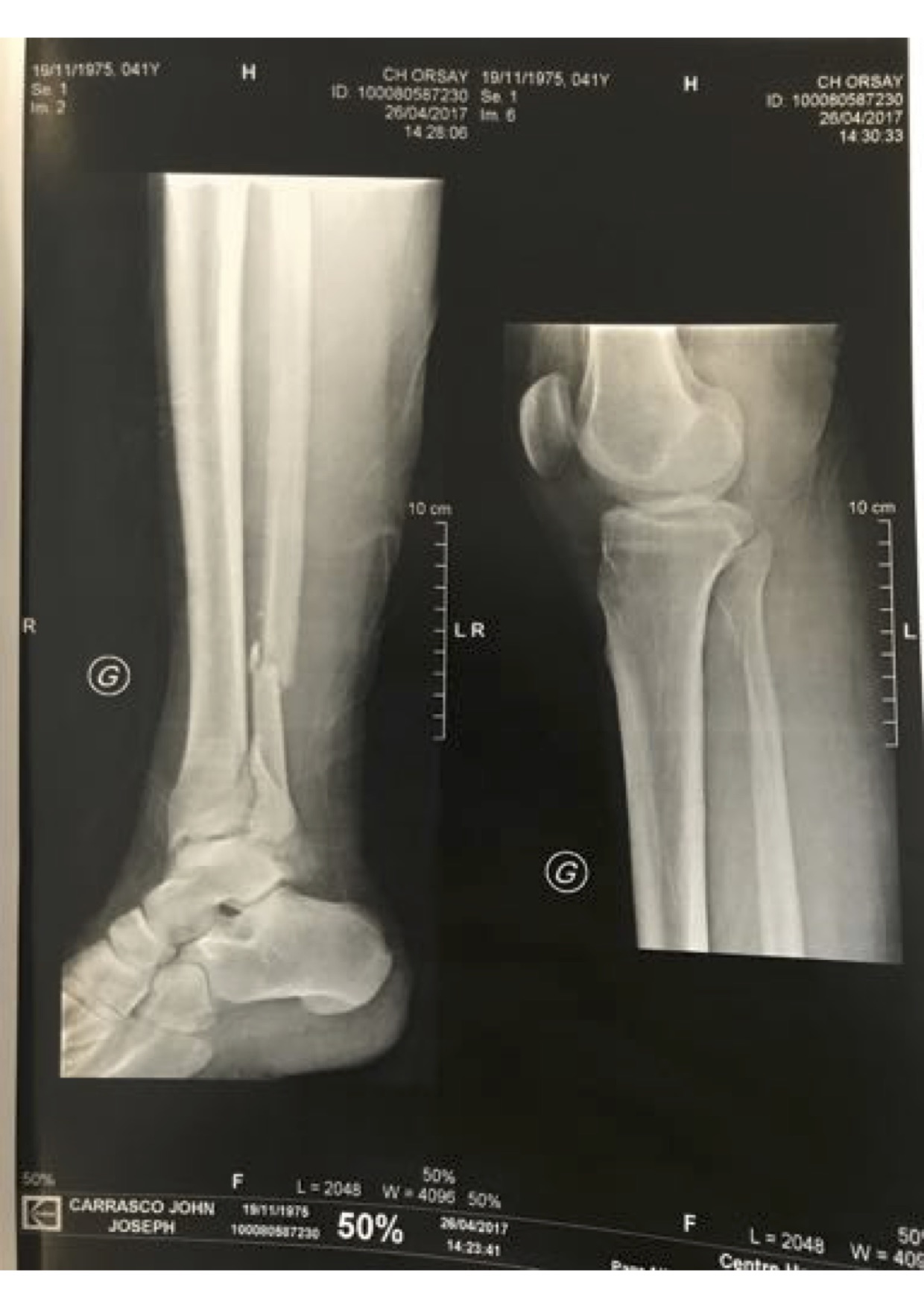
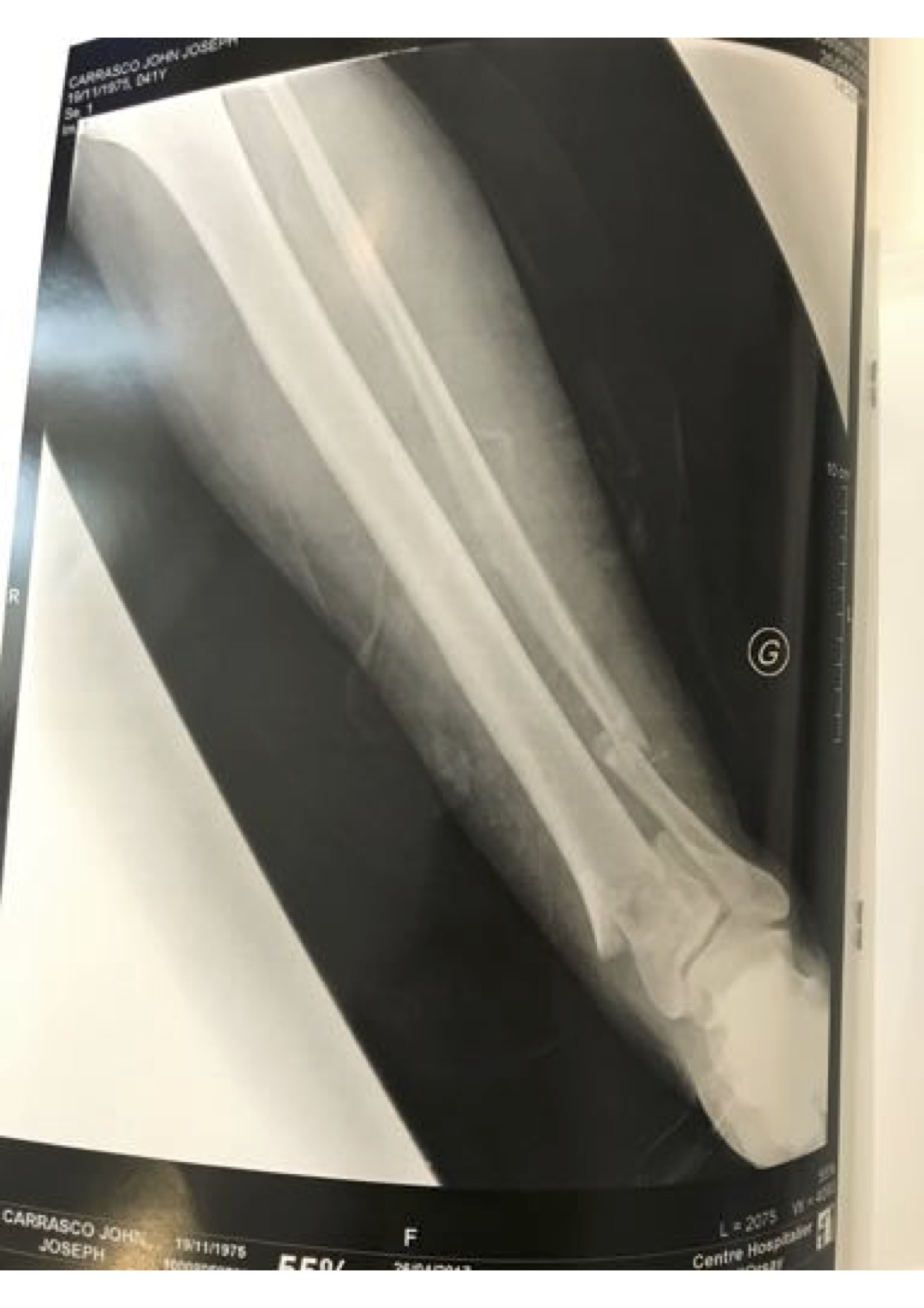
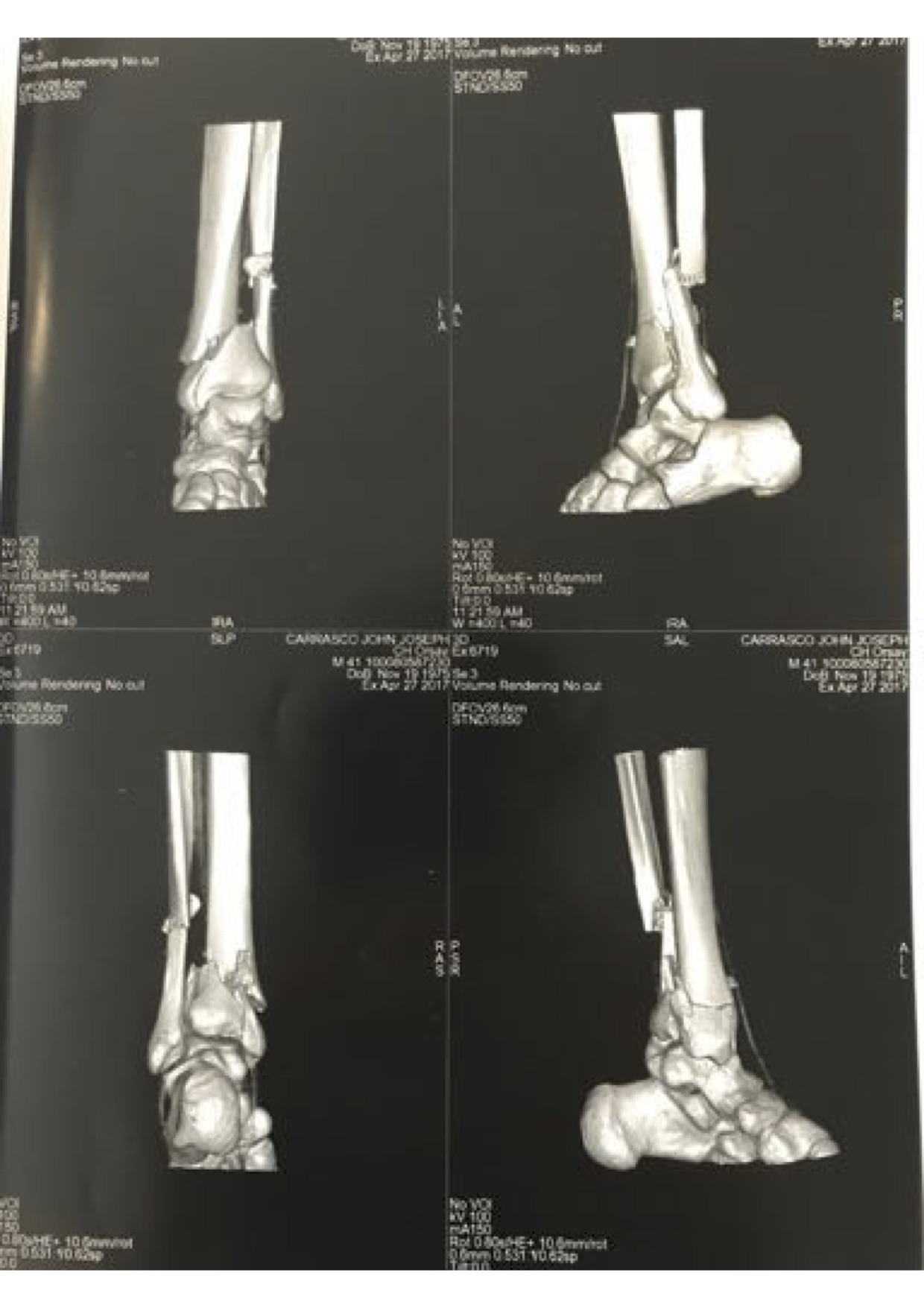
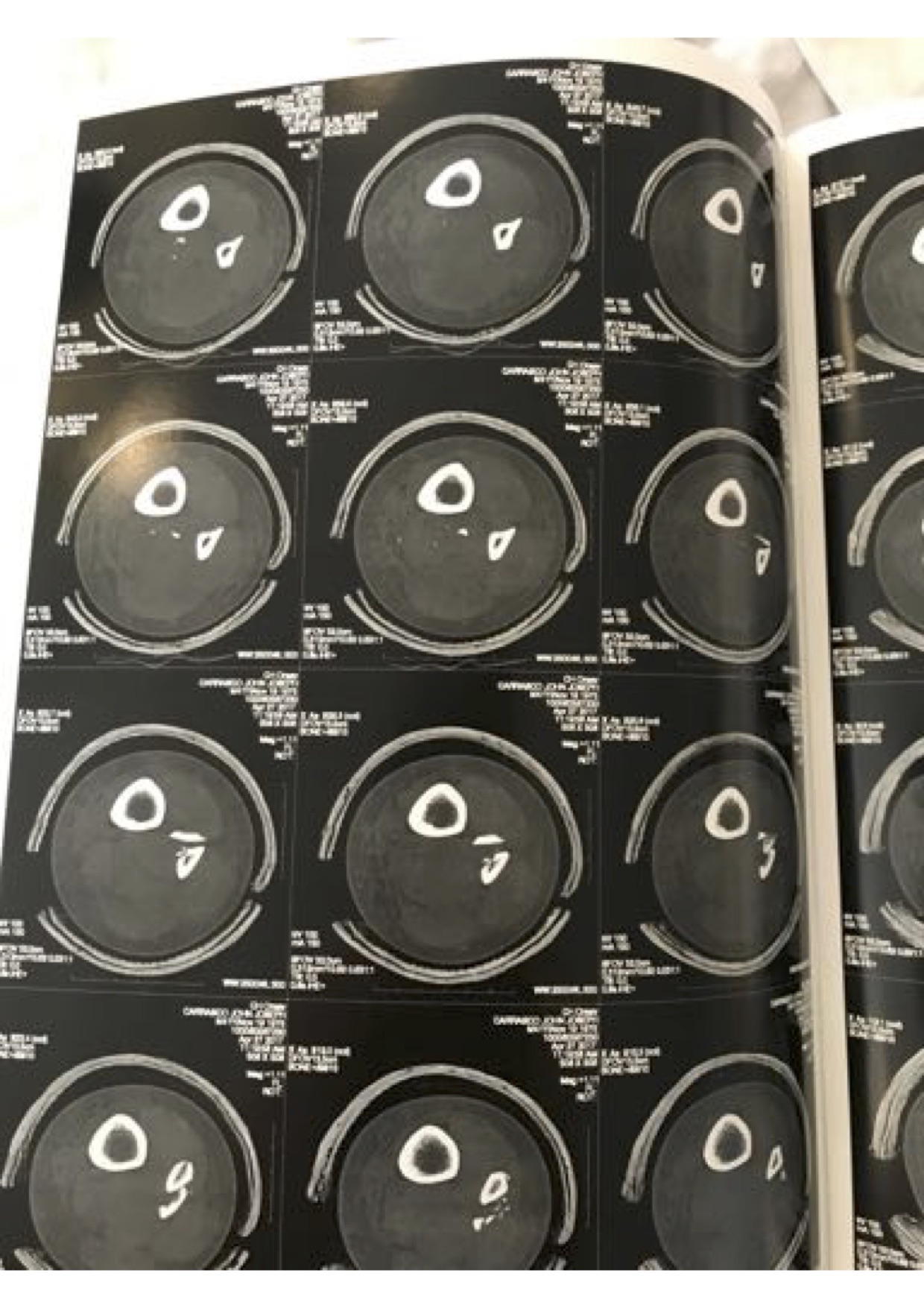
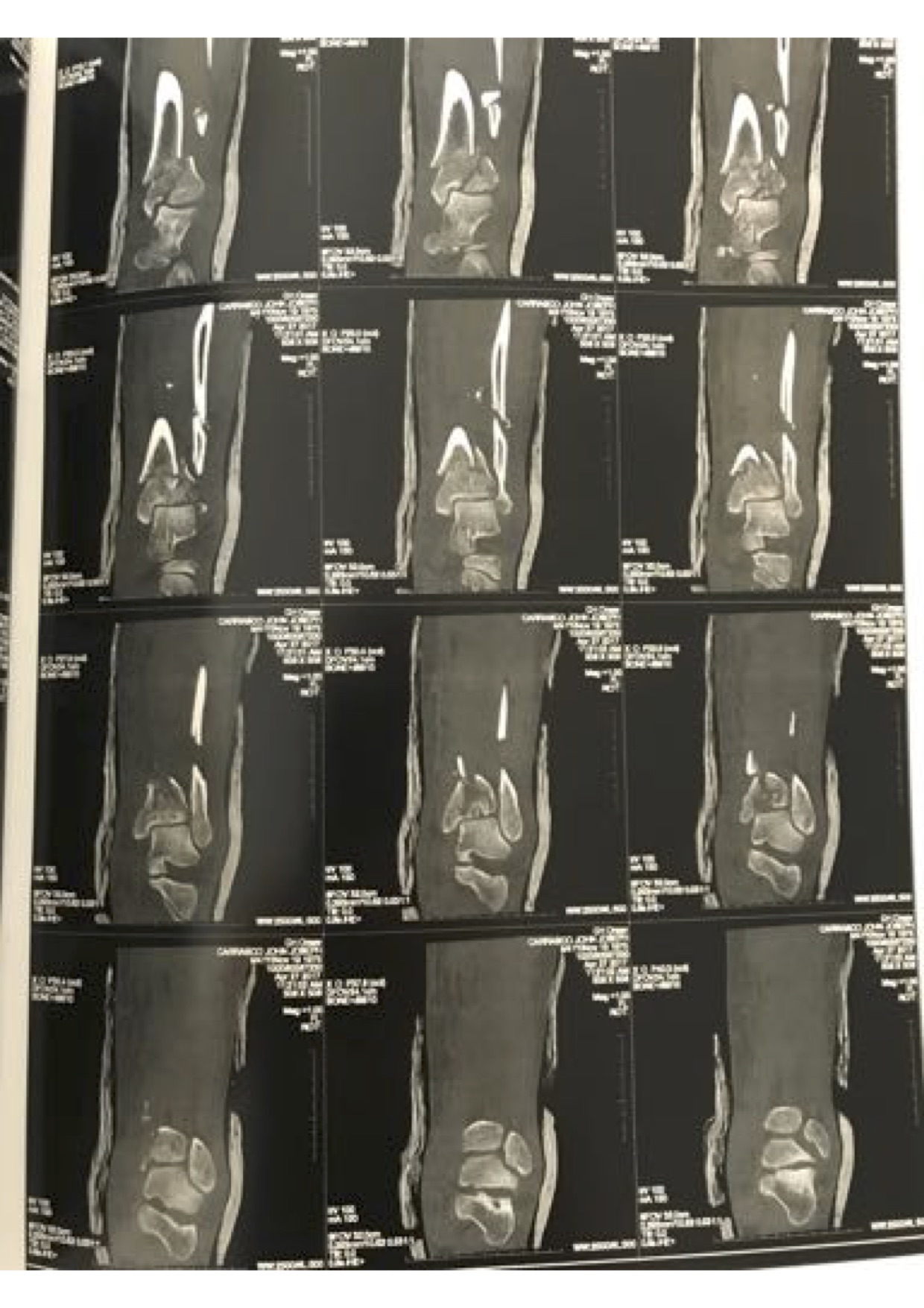
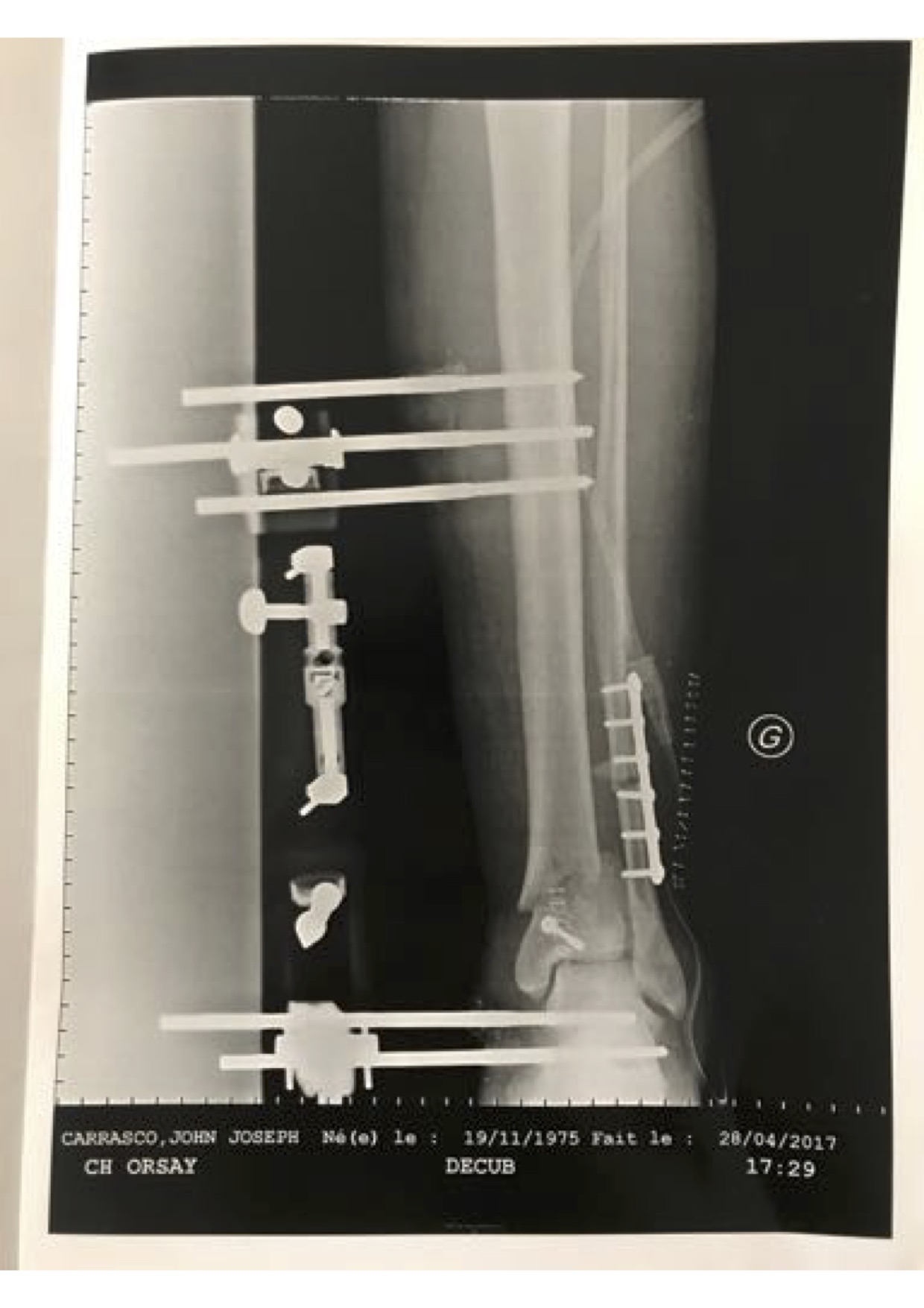
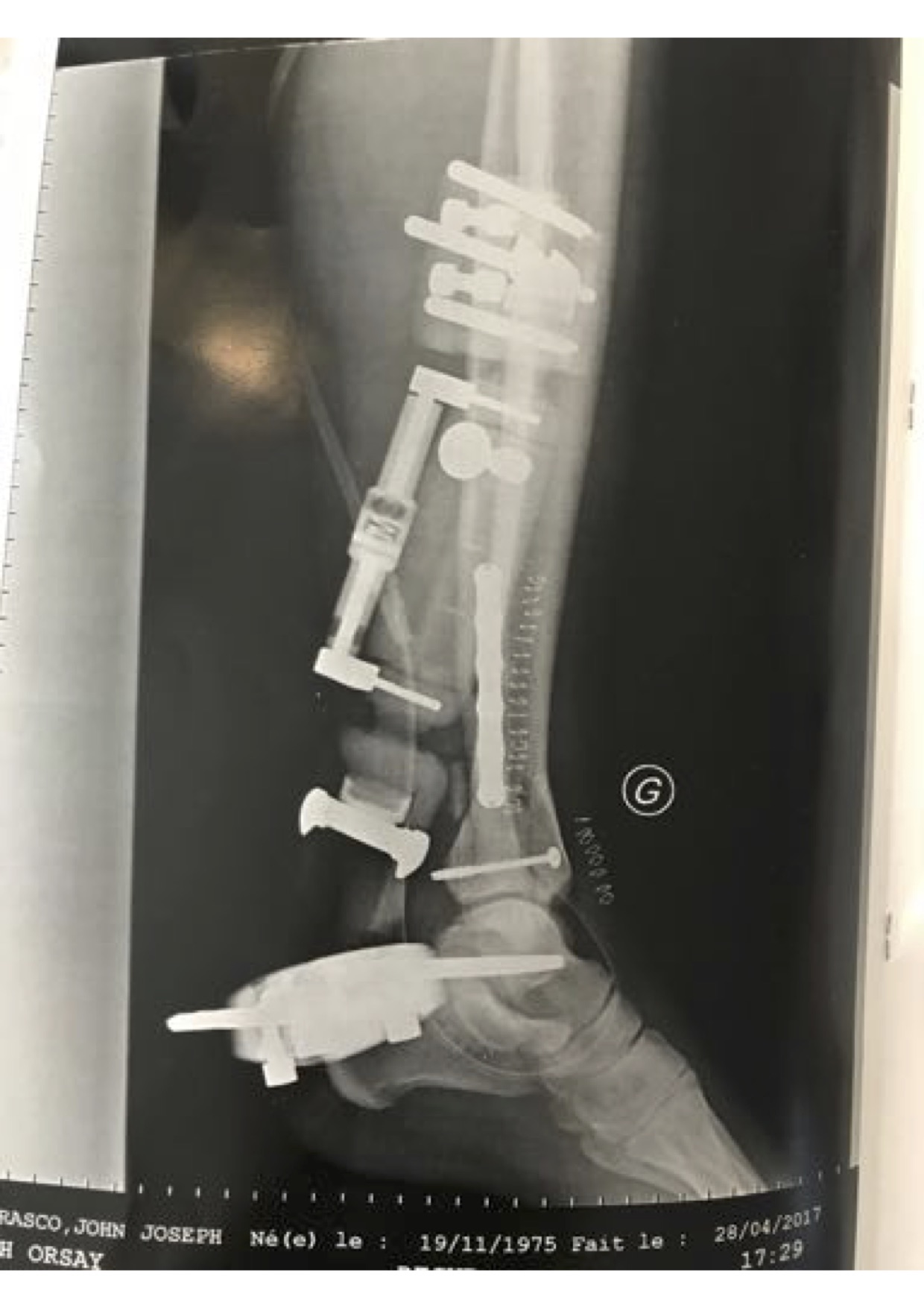
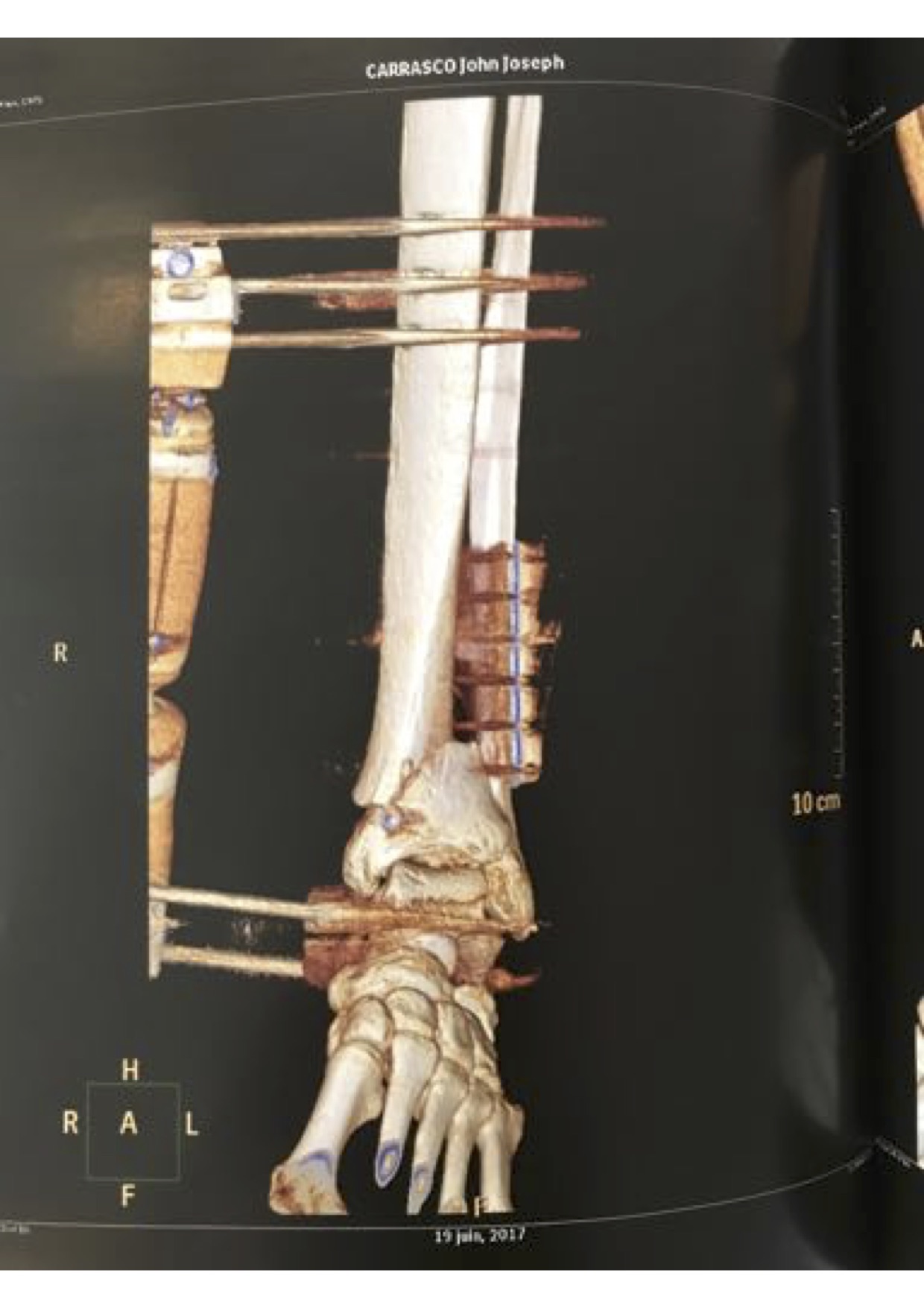
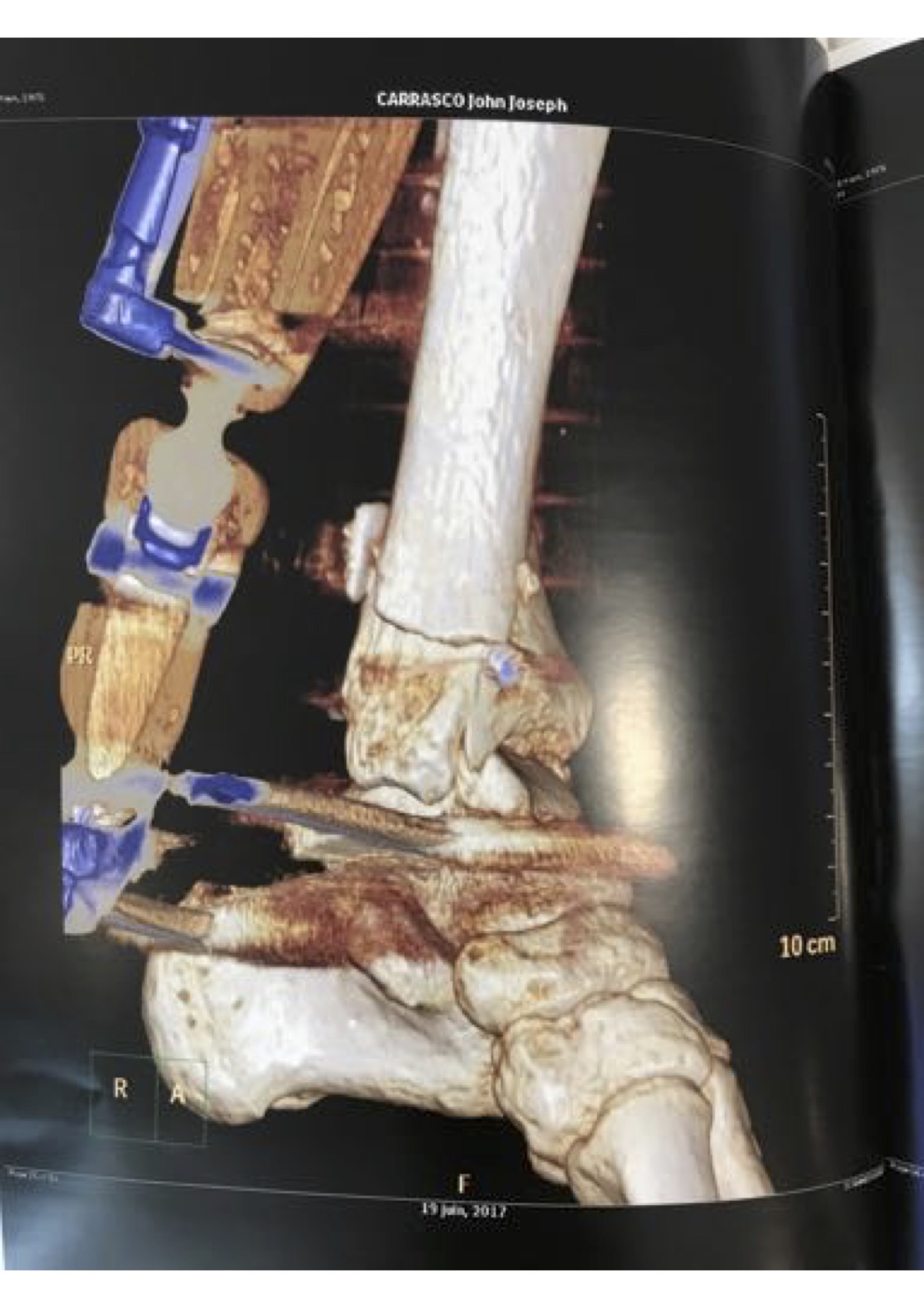
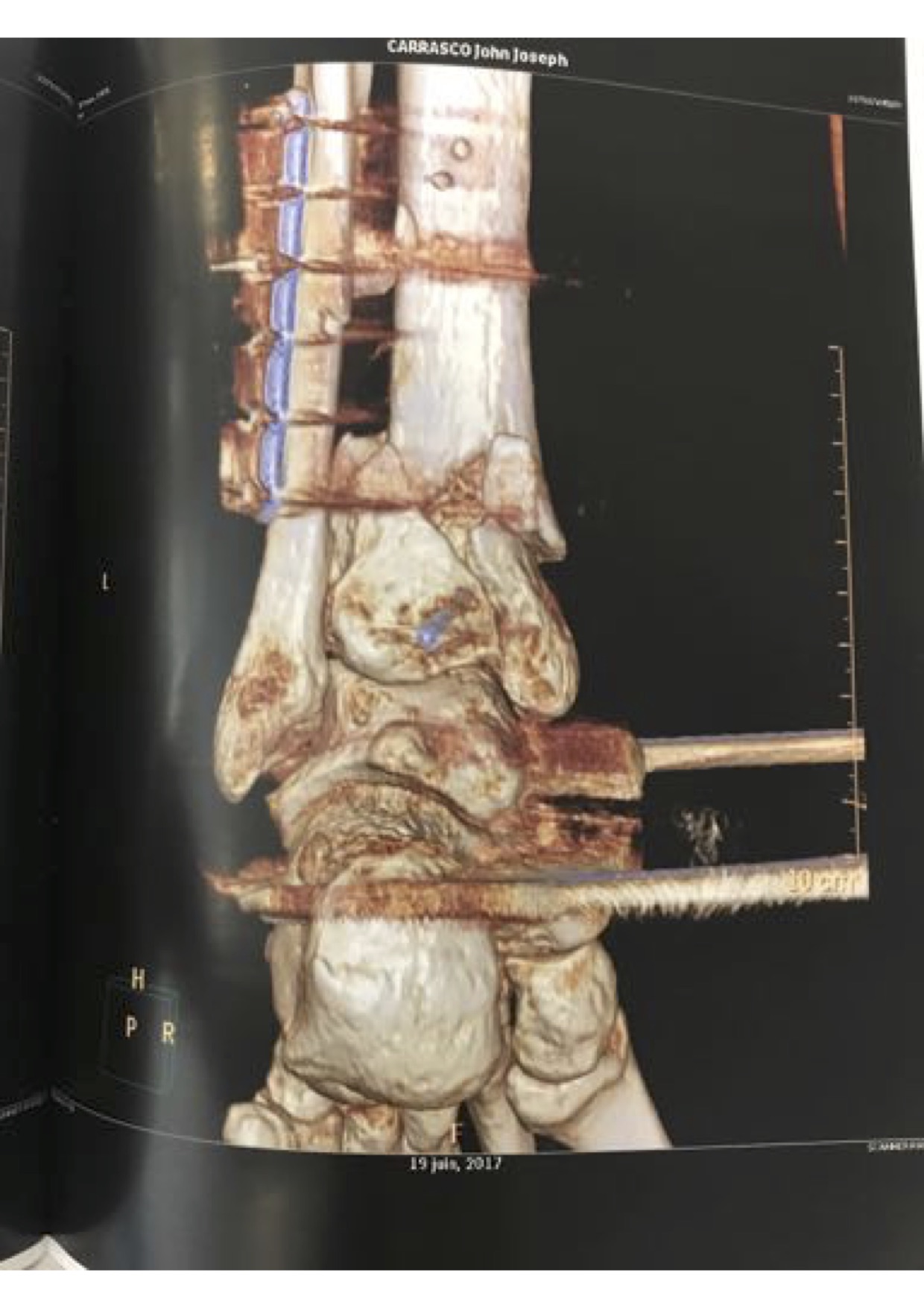
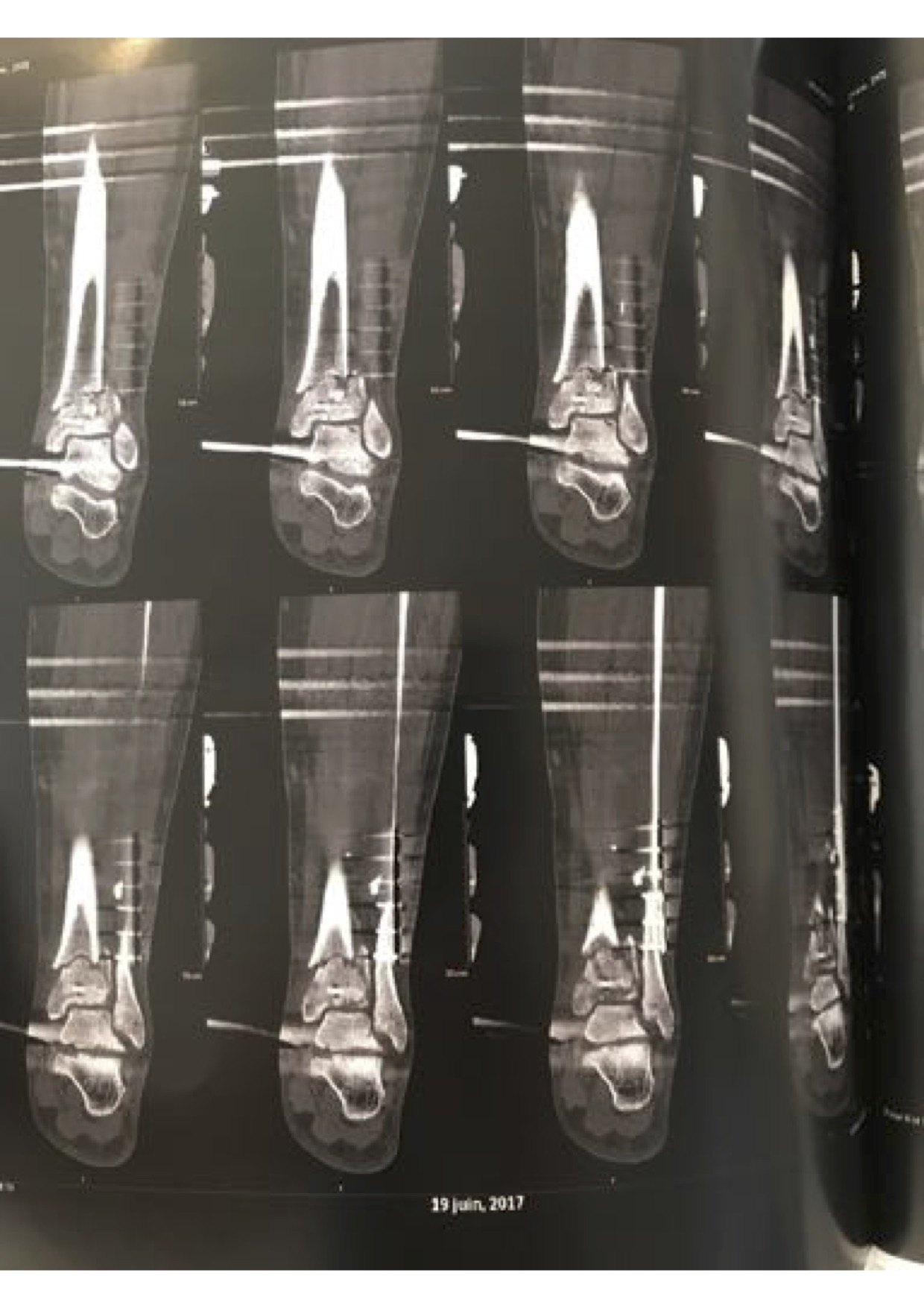
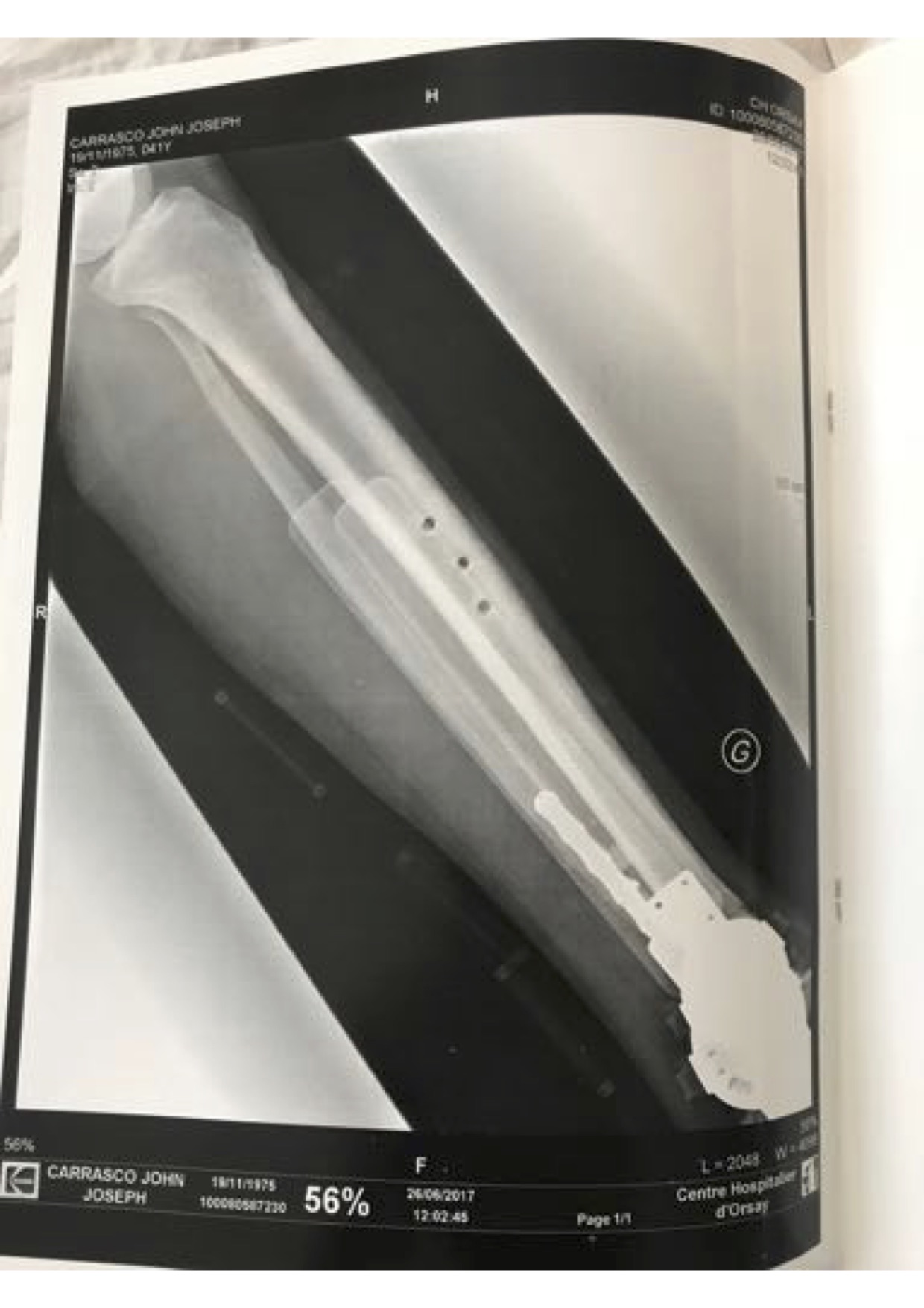
My grandfather Vincent Carrasco ( just turned 100 yesterday!!) has been working with a physical therapist, Bradford Matalon. Mr. Matalon took a look at the x-rays when my folks were visiting Long Island, and had some exercise suggestions, which he generously agreed to let me share.


















Video for [Lecture 1] [Lecture 2] [Lecture 3] [Lecture 4]
Link to all summer school lectures, hosted by the Higgs Center for Theoretical Physics in Edinburgh, here.
Other lecturers: Stefan Weinzierl, Marcus Spradlin, Jaroslav Trnka, and Johannes Henn.
Also nice research presentations by: Jorrit Bosma, Sebastian Mizera, Gustav Mogull, Chia-Hsien Shen, Andrew McLeod, Theresa Abl, Joe Farrow, and Andres Luna-Godoy.
Introducing graph methods for modern amplitude calculation. Topics:
Graphs and Ordered Amplitudes
Integrand Verification – two-loops.
Integrand Cut Construction – two loops.
Introduction to Color-Kinematics
Unsatisfactory tensile strength of one leg, combined with a fairly local interaction of a skateboard and an ill-chosen hill on a novel commute route, necessitated a little creativity in lecturing – black boards are out for at least another month. I didn’t want to present a straight-up slide show which I find a little off-putting for lectures. Rather I decided to (for the first time as a lecturer) live-generate a Mathematica notebook as the projected lectures. Obviously this could be incredibly off-putting, but this I indulged, as it’s the type of thing I would’ve loved to see when I entered this field in 2006.
Indeed, I organized around what I had to do as a early-stage graduate student to think through and understand the graphical mechanics behind the first paper that made sense to me re: the unitarity method – the groundbreaking 1998 two loop maximally supersymmetric supergravity calculation of Bern, Dixon, Dunbar, Perelstein and Rozowsky. You can find the paper here.
I start by introducing the need for graphs with structure to encode the types of minus signs that show up around vertex flips for adjoint color-weights. I explain how to generate the graphs contributing to unitarity cuts and how to dress them with a candidate graphically organized integrand (mapping from graphs to weights). We poke at what’s necessary to constrain a graphically organized integrand to match a given theory, and at the end delve into constraints that have nothing to do with physical observation but have everything to do with lining up local stories relating gauge theory and gravity predictions.
I did a little post-cleanup to make it somewhat more readable for people who don’t get to hear my vocalizations, but have posted sooner rather than indulge ever-present obsessive impulses towards stand-alone readability.
I don’t emphasize it but I’ve dropped in some pretty chonto casually tossed off calculations like automatically taking gauge integrands to symmetric double-copy gravity cuts via KLT, and evaluating 4D state sums for generic cuts in choose-your-SUSY gauge theories at the push of a button. As these weren’t (primarily) graphical methods they weren’t central to these lectures, but I can probably be tempted into writing some words about them at some point.
Notebook uses my github hosted amplitudes graph library ampGraphTools. (No need to install the library, it imports directly from github if the lectures’ notebook is executed.) Presented with an emphasis on output, not so much on code/library use, but does provide a slice of insight into how I actively think through this graphical playground when I’m poking about.
As a side note, I saved the notebook periodically throughout my lecture, and had it temporarily hosted on a dropbox folder accessed via a bit.ly link for students to grab as they liked. Interesting to see the stats of how many students bothered to grab the notebook vs who couldn’t care less.
Definitely welcome any questions, desire for clarification, and requests for any topics I skipped in this limited lecture time.
]]>Standard `quick note’ disclaimer: This is almost entirely stream of consciousness analysis with all the incident depth, insight, consistency, and utility one can expect.
Every so often I notice a flurry of discussion among my scientist friends on twitter.
“Impact factors are no basis for a career; young folks shouldn’t pay attention – worry about the quality of the research!”
This is so manifestly correct it’s hard to imagine anyone can question it. If you try to even have this conversation with a theoretical physicist it just falls on the floor – there’s no interest in debating it at all. I’m going to take a minute or two to poke at why.
First it’s important to realize that formal theorists barely notice journals at all. This isn’t new. Since the advent of the arXiv they’re irrelevant2 for
Why wait on the judgment of a handful of other folk to bless the possible keys to the universe when you can just read the preprint yourself. If you can’t understand the paper you probably are in no position to judge it, so offload. What if for some random reason you need to measure the importance? I can’t count the number of times I’ve heard (and probably said), “What the hell, if you’re too lazy to bother reading and understanding a paper4, just look at it’s citation count5 for impact, that’s what inSPIRE is for!”
Obviously I’m not going to justify laziness, but at some point–really early on–I came to live with the second bit. Citation count, assuming a sufficiently honest community, is a measure of impact. Is it fair? Absolutely not; people who have higher visibility – socially, or because of past performance, or because of what institutions they’re at, or have a more favorable gender/cultural/ethnic presentation, or because they invite themselves to talk everywhere, or because of who’s their advisor/best-friend/sister-in-law, etc. – are better read. As my former Ph.D. advisor continuously emphasized to me (and still does every time I grit my teeth)
“There is no justice, only luck.” -Zvi Bern
And Zvi’s right – in academia, as in life, there’s no justice, at least none you can count on6. I’ve seen awesome proposals go unfunded, and spectacular candidates go un-hired, and you can trace out why, and it has nothing to do with justice – in the end, it’s bad luck. Well bad luck and herd mentality. But independent of whether citation count is fair, it does demonstrate whether papers are leading, following, or irrelevant to the zeitgeist. Does that define good papers? It depends on what you mean by good – high citation count certainly suggests they’re stirring the pot and that’s necessary for science to progress. If you really want to know if a paper is good for you, read it and see if teaches you something (or model whether you think it would teach something to those poor unfortunates who aren’t yet as brilliant and insightful as yourself), if it does and you care about what you learned then the paper’s done something. If not, well…
But sometimes you don’t care about whether a particular paper is good, you just want a quick hack to see if someone’s work has impact. Anyways, I internalized citations as impact almost the second I stepped back into academia – it’s just manifest. You can’t measure impact on a short time-scale, and so take a long enough time scale, and see whether something makes waves. It honestly doesn’t even occur to mess around with silly proxies like average citation count in a time period by a journal. Small citation numbers, over short time scales, are going to be noisy and uncertain (could be errors, could be lack of luft, etc), over longer time scales and especially as numbers build up, they tend to stand on stronger footing.
I have to say one of the hardest things about leaving industry and returning to academia was the new time-lag of the feedback loop re: “are my ideas any good???” In my previous life, actually working for a living, the feedback was almost instantaneous, and completely unambiguous: “Does your idea make more money7?” Even for subtle questions the feedback loop was on the order of months, because who in industry has the luxury of longer-scale strategies? Academia doesn’t have such rapid time-scales. It can take months to years to see if your ideas take root and flourish in the community, so you just get used to it, and you develop your nasal acuity to sniff out whether certain questions smell like they’re worth pursuing, and build the requisite self-confidence/hubris to actually trust your own judgment.
Ahh, but what about jobs – how can you wait for citation impact to decide on jobs? Well there are are a few things here:
There are typically two if not three 3-year postdocs these days between Ph.D and tenure-track positions in theoretical physics. Combine that with the sheer volume of Ph.D’s being produced and post-docs competing for positions, not to mention the output of our glorious high-drive hires over the past \(X\)-decades still producing at a tremendous rate, we have a flood of data. There’s a fair bit of time for people to build up their street-cred, and enough people generating papers that you don’t have to wait all that long to see if people care about what you’re doing.
Is this healthy? I don’t know – a lot of permanent hires these days are spectacular8. We “lose” fantastic people to industry, people we’ve invested a tremendous amount in training, and people who have given us tremendous energy, ideas, and stimulation. This is one reason we should all work towards making the transition between industry and academia much more two-way at all career stages. We should invest in leveraging those industries that benefit from our training, to help support general soft-term research positions, and relevant research programs in general. We additionally need to create space for our relatively newly-industrious academic children to maintain their connections and share their time and energy to the scientific endeavor on their personal time-scales. Not everyone wants to teach, nor should they. Researchers like to research – and they can enjoy, it turns out, solving many different types of problems. But this is also a topic for another day.
I can imagine in fields where there’s a lot less being written, where journal peer-review slows the visibility of impact, and where you’re expected to land a job in reasonable human-life-scale time periods, journal impact factor might seem relevant (even if everyone agrees it’s hyper-crappy). On the basis of absolutely no evidence, I suspect such fields would be even more susceptible to the whim and whimsy of key established players, so looking for anything that seems like hard data would be attractive. This isn’t us – we’re sitting on tons of impact data (whimsy driven as it may be), and are conditioned into seemingly infinite patience.
So why did I write this if we never have these conversations? Largely, while wondering why I was seeing it on twitter again, I finally stopped to consider how distinct our culture may be in academia, and thought I’d share9. Happy to learn from anyone else’s experiences, similar or varied.
Yes, I’m that old. Whaaaaazzzzuuuuuuppp! ↩
I’m not asserting, as many of our young firebrands will, that journals are useless. I think the role has changed – it’s now a lot less about getting jobs, and – when useful – more about promoting good science. Sometimes it’s nice to know at least one person was forced to pretend to read one of your papers – I’ve learned a lot about broadening my scope by well-intentioned and absolutely mystified referee reports. Even better are when people actually catch honest glitches. That’s great, I’ve heard ;-). Moreover, as a referee I appreciate having the excuse to dive into papers I’ve been meaning to spend more time with (typically multiple weeks after first browsed on the arXiv). Note: these are different circumstances than public comment threads on papers, which are fine, and should not be on the arXiv. I may have a more in-depth discussion of refereed journals at some other in-between time. ↩
Since talks are now widely posted and archived, sometimes even the arXiv is subdominant for priority. Feel free to look at my articles to see how many times I cite Michael Kiermaier’s Amplitudes 2010 talk at Queen Mary University. ↩
Which we all agree is TOO LAZY. ↩
Don’t worry, I’ll get to visibility privilege and citation count in a bit. Keep going. Or don’t, I’m killing time in a hotel room here. Now…I’m killing time in a lobby. ↩
Though in academia, as in life, it is worth striving for! ↩
Somewhat joking – it can often not be directly about money – but it is about a metric you should be moving on a very short time period: impressions / user-base / satisfaction / conversions…that will eventually be linked to money. ↩
With entirely obvious inclusion issues for anyone bothering to glance around (cf. visibility above). ↩
Meant for a broad audience, giving a “big picture” overview of a thread running through the amplitudes community. Attempts to gently introduce color-kinematics, double-copy, geometric picture, generalizations that let us get to 5-loops maximal supergravity, playful constructions like Z-theory, and applications to classical solutions.
If it were up to me, I might have chosen a slightly different freeze-frame for the video ;-)
Slides posted:
Here’s the Mathematica code I used to scrape inSPIRES to build a weighted display of authors who cited a particular paper. Need to have the inSPIRES recid (can read off the url after clicking on the paper).
Ugly hack – might be ameliorated if I could find any docs on inSPIRE’s API.
Usage:
getAuthorsForPaper[635599]// Sort (* 2003 Witten's Twistor String paper *)
First few lines of output:

An early contender was “Advanced” Theoretical Physics, in the computer-aided spirit of Advanced Chess. Unlike some of our antecedents, I don’t view engaging symbolic processor neural-adjuncts as some sort of intellectual juicing1. Indeed I’m more than happy to automate any aspect of my inquiry towards improved:
Both of which up the chances of discovering something truly interesting. I’ll likely be writing more about all of these soon.
But as much as I enjoy the ever increasing meta-cognitive aspects of engaging our silicon friends to aid in the quest for deeper knowledge, I don’t really think of this as a central enough tenant so as to be defining.
Also, and all things being equal, it’s worth considering the following point: using the word advanced to describe one’s own work is the type of thing that tends to piss people off. I’m preternaturally pleased with myself whenever I realize there’s an opportunity to avoid arbitrarily aggravating my colleagues. So what should my group be called?
A common trope is that theoretical physicists ambulate about dreaming big dreams. Sure we do. But what we work on is making predictions: some very formal like the high-energy (small-distance) behavior of supergravity. Some are highly phenomenological like early Dark Matter evolution towards the cosmological formation of Large Scale Structure.
My group doesn’t shy away from technically challenging problems – rather we see them as providing strategic pressure to push our current ideas, tools, and interpretations to their failure-point. Yet, every calculation we do is driven by a deep curiosity. Every time we gear up for one of our analytic “experiments” we do so because we expect the theoretical data we extract to be invaluable. So while we’re partial to calculating, it’s the resulting data we’re interested in; the journey might be fun, but in our case we really are interested in the destination.
Physicists like to get to the nub of an issue – simplifying away the stuff we don’t care about to get to the heart of the stories worth telling. Even when you’ve simplified away all the details you think are garbage (relevant to what you want to explore) you’re often confronted with some differential equations whose solution may have important properties you don’t sufficiently appreciate.
Let me make an aside here about solutions and differential equations. Did I say “confronted with diffEQs whose solution you do not know?” I absolutely did not! I hope the following tautology is obvious to everyone: By specifying some (set of) differential equation(s) you’ve implicitly specified the class of solutions. Ever since my volatile youth, it always got under my skin to hear people say they don’t know the function that solves a differential equation. Differential equations tell us how functions behave – what else could anyone want in a solution??
Let’s just consider a simple example that’s in a very real sense (with a slight generalization) kind of behind everything: \(\begin{align} \partial^2_t f(t) &= -f(t) &f(0)&=1 &f'(0)&=0\\ \partial^2_t g(t) &= -g(t) &g(0)&=0 & g'(0)&=1\\ \partial^2_t h(t) &= -h(t) & h(0)&=1 & h'(0)&=i \end{align}\) By knowing nothing beyond the boundary conditions and the differential equations, it turns out we know a tremendous amount about these functions. For example we know that \(g' = f\), which in turn means that \(f'=-g\). We know that \(h(t)=f(t)+i g(t)\). Cool. But there’s more fun to be had. Note that \(|h|^2=f^2 + g^2\). Taking the derivative of both sides: \(\begin{align} \partial_t(|h|^2) &= 2\, f \,f' + 2 \,g \,g'\\ &= - 2 \,f\, g+2\, g \,f=0 \end{align}\) which means that \(|h|^2\) is constant. Since \(|h(0)|^2= 1\) this means \(f(t)^2 + g(t)^2 =1\). This is a spectacular result at the heart of trigonometry! (Of course you’ve already realized that \(f\) is the cosine function, \(g\) is the sine function, and \(h(t)=e^{i t}\)).
Can we go further and derive those pesky trig identities from middle school? Of course we can – but let’s leave that as an exercise to the reader. From just considering these differential equations we know everything about these solutions except perhaps how to get numbers out. But in fact we even know this, recalling our Taylor expansions: \(\begin{align} f(t)&=f(0) + t f'(0) + t^2 f''(0)/2! + t^3 f'''(0)/3!+\cdots\\ &=1 -t^2/2 + t^4/4! -t^6/6!+-\cdots\,. \end{align}\) Which has taken me…
back to perturbations…
If you don’t know sufficient properties of your (implicitly defined) solution to claim you know the solution, you can still get numbers out – predictions. If you can find some parameter that is small enough you can expand around it and go after approximate solutions whose errors are parametrically controlled. In fact I’ll go so far as to say:
All physical solutions (even “exact” solutions) are perturbative in the crap you don’t care about.
The tricky bit is when you care about the stuff that makes your life complicated – but in this case we can try to expand about the complications. A lot of our calculations are organized into formal expansions around some parameter which we then typically take to be small. Why small? This is so that successive orders are parametrically suppressed and can eventually be neglected in prediction. The above formula for \(f(t)\) is true to all values of \(t\). Something nice happens with the numbers for \(t<1\) — I don’t need to go very far in the expansion before \(t^n<<1\).
In any case, this is called a perturbative expansion as we imagine these corrections as small changes or perturbations to the leading order solution given a small enough parameter. This is great, and a handy thing to have in one’s tool belt. But again, it’s not so much the tools as why we’re going after the problems we do. I’m not exactly sure what the point of a theory group’s name is, but one might hope that it coordinates towards the type of physics one aspires to do.
The more that I thought about it the more I realized that most of my approach is marked by the simultaneous presence of two attitudes. I have a tremendous amount of trust in the what – the invariant predictions – independent of choice or framework up to parametrically controlled error. I’m much more skeptical about the ultimate truth of the stories – the how (think Lagrangian’s / Hamiltonians / particular gauge choices / which spectator or auxiliary fields we allow and which we integrate out etc) – that let us arrive at these predictions.
I believe in predictions up to the point that they are consistent with actual observations. I tend to think of the stories we have so far developed behind them as effective just-so tales: grasping, yes, some essence of truth, but certainly not the only or ultimate way the universe behaves. Of course I’m deeply impressed by the ultra-soft UV behavior of our favorite extended theories, or even the renormalizable behavior of our miraculous pointlike non-abelian gauge theories. Does that mean I really believe they hold to all—or even any—scales beyond which they’ve been observed? I think it’s possible, but I also expect surprises from the universe.
It’s absolutely possible to discover startling new structure unifying theories that have been at the heart of modern physics for decades and decades. I believe as we gather more theoretical data — the what — and we give ourselves the space to play with different compatible stories, we’ll find ever more efficient, and ever more meaningful how’s. It’s this focus on the what, allowing a freedom in the how, that ended up suggesting the group name I finally decided on.
I’ve taken this inspiration from a certain paradigm of programming – a functional one, where the idea is to write algorithms focused on the logic – the objective – and not so much the control-flow – how it gets done. This is called “declarative programming”, and so it is in that sense I give you the Paris-Saclay Group for Declarative Theoretical Physics.
That said, I’m completely willing to back a proposal for a straight-edge arXiv sub-branch for research performed with neither Mathematica nor caffeine. ↩